Making an air powered cannon

I want to shoot a projectile fast.

That has been my main aim for years: to track the speed of a projectile that I shot, and calculate a speed of over 100mph. Unfortunately, as I live in the UK, I cannot do this with gunpowder, and using butane or gaseous propellant still counts as a firearm after the projectiles start reaching certain speeds.

For a while, I was stuck, until I realised air cannons weren't legally registered as firearms. I have always wanted to make an air cannon, but every attempt I made ended with the same result - failing to form a perfect seal. The issue was that a small leak would always be present, and at higher pressures of around 30psi, the rate of air leaking out of the bottle was equal to the rate of air entering the bottle through my pump, leading to a maximum pressure that I couldn't circumvent without expensive gaskets and O-rings. 

However, with my newfound access to a 3d printer and 3d modelling skills, I can make custom parts. This avoids the need for seals and joints that I would've otherwise had to make with low tolerances and shabby materials.

Firstly, I found the thread dimensions and schematics for soda bottles in the UK. I decided on soda bottles as they have a maximum pressure rating of almost 150psi, which is more than enough for my goals.

This gave me the cruicial information that the diameter of the bottle neck was 27.4mm, and the thread pitch was 2.7mm. I 3D modelled a tube that would screw snugly onto the threads of a soda bottle neck, with the same threads as the cap. There is a ridge at the end here, to allow a burst disc to be fitted so that it is pressed tightly in place between said ridge and the end of the neck of the bottle

 

 

I then converged this section down to a diameter more suitable for the barrel of the cannon, which would be made of 15mm PVC, with an external diameter of 22.1mm. This would have two holes in it, opposite eachother, to allow a screw to go through that would secure the barrel in place.

 

The barrel of the gun would be friction pressed in here, with a thin layer of superglue to keep it in place, and finally two screws drilled in to ensure it never gets pushed out under pressure. I planned to drill a hole in the slanted section to allow myself to fit a bicycle inner tube stem valve, which would reliably hold pressure, and easily allow me to pump up the bottle with a bicycle pump that has a built in pressure meter. 

 

 

 

A couple of minutes before I sent the 3d printing files, I realised I had made some major mistakes, chief of which was having the input for the air pump after the burst disc. This meant air from the compressor would attempt to pressure an unsealed barrel, and no air would actually enter the bottle itself. Secondly, the threads on the inside of this part were longer than the bottle neck itself, so there would be no way to screw it in enough to squeeze the burt disc itself.

 

To remedy these issues, I split this part into two pieces, with one piece being dedicated to the PVC barrel, and the other piece being dedicated to the cap and pump. The part for the cap and pump was hardest to model and had the most engineering constraints.

You may ask why there are two input holes, and this is because I decided to introduce a safety pressure release valve. When using the stem of a bicycle inner tube, it can be difficult to remove the bike pump, especially when the apparatus is pumped up to high pressure. This would also require fiddling around and pulling on the valve, potentially leading to a catastrophic rip somewhere in the system. 

 

 

To avoid this, I found a FASTGAS cylinder by the side of the road, and after thoroughly cleaning it up, I used a wrench to unscrew the ball valve it had on the top, rated for 1200psi. When pressed, this would dump all the pressure in the bottle extremely quickly, with very little force, since we would only be running it at 1/12th of its designed pressure. The reason the sides of the part are flattened is to allow the O-ring on the back of this valve to have a flat surface to 'squish' against and form a perfect seal.

This is the other part that completes the assembly. The smooth section is where the PVC pipe is glued, with markings to designate where nails can be drilled into to secure the PVC barrel even more, akin to the previous iteration. The threads on the back of this are designed to coincide with the larger threads in the previous part, with a flat rear profile to ensure that the burst disc is squeezed tightly in place.
 

Unfortunately, this part only went up to the manufacturing process, where it promptly failed - this part was not going to be easy to 3d print - borderline impossible with the cheap 3d printer I had access to, so it was back to the drawing board.

 

I had to completely remodel the part so that it could be 3d printed. One limitation of 3D printers is overhang. 3D printers work by heating up some plastic and running it through a filament, which heats it up into a liquid. The printer then moves through a set path, depositing this liquid on top of something else, then waiting for it to solidify. It does this layer by layer until an object is made. This can be thought of as putting hot glue on a plate, waiting for it to harden, then putting more hot glue on top to make it 3D.

 

The issue with this is that to make the part, the printer needs to deposit this gel-like plastic on top of something else, or it would just drip down, like honey from a bottle. Most modern 3d printers can deal with overhang angles up to 45 degrees, which means that a shape like this can print perfectly:

 

While a shape like this will print badly, or not print at all:

 

 

An example of this dreaded phenomenon is shown below:

 

 The common way to solve this is to use supports, which serve as a 'scaffolding' to allow the melted plastic to stay in place while it solidifies. The supports are made porous and weak, so that they can easily be snapped off after the print to leave you with the desired part. This porosity leads to a fatal downfall in this use case, where we need an air-tight, strong chamber.

 

The next design was built with 3d printers and simplicity in mind.

 

After inspecting the cap of a soda bottle, I realised most of the seal didn't come from the threads of the bottle themselves, but from the tight squeeze between the top of the bottle's neck and the underside of the cap when screwed together. To utilise this design in my part, I modelled a ridge directly after the threads, so that it would be tightly squeezed when screwed on.  hopefully forming a seal. The ridge is angled at 45 degrees to allow it to be 3d printable without supports, and also to be able to hold an O-ring in place without it slipping out.

 

Moving up the part, we can see that the 'lid' is now tapered up in a conical shape. This allows the part to be printed without supports running through it, maximising the amount of air flow that can rush behind the projectile in a unit time, effectively increasing efficiency by lowering the drag coefficient of the inside of the cap.

 The whole part, in section view, looks like this:

And everything in tapered at 45 degrees, even the little ridge visible in the left tube. This design is an incredibly simplified version of the first. The PVC tube is pushed into the top of the tube on the left, and stopped by the ridge. A burst disc is placed under it, and the right tube is screwed tightly onto a bottle, which is pumped up. This pressure is transferred to the left tube via a triangular exhaust hole that links both chambers together. It is shaped this way, like everything else, to avoid supports being used in the print. Note that the hole in the top of the cone on the right is to thread a Schrader bike valve, to provide the pressure.

The final part looks like this, with the dark blue shape simply being a reinforcement, as simulations showed that the intersection between the two pipes had the highest stresses:

 After 3d printing, drilling, and installing the valve with the suitable O-rings, I had this:

 The two holes on either side of the PVC holder are there so that a bolt can be threaded through the PVC pipe aswell, to stop it popping out under high pressure. With a PVC tube cut to length and with two corresponding holes drilled through, I was left with this:

 Finally, with the bottle screwed in:

This is a CAD simulation of what an ideal projectile would look like being fired from this air cannon:

 

After this was assembled, I coded a Python Script to estimate the muzzle velocity, and find the optimal barrel length for it:

You can use this version interactively right here on your browser - click the triangular 'Run' button, then input the data the program asks you for. Here are some good default values that are realistic for this air cannon:

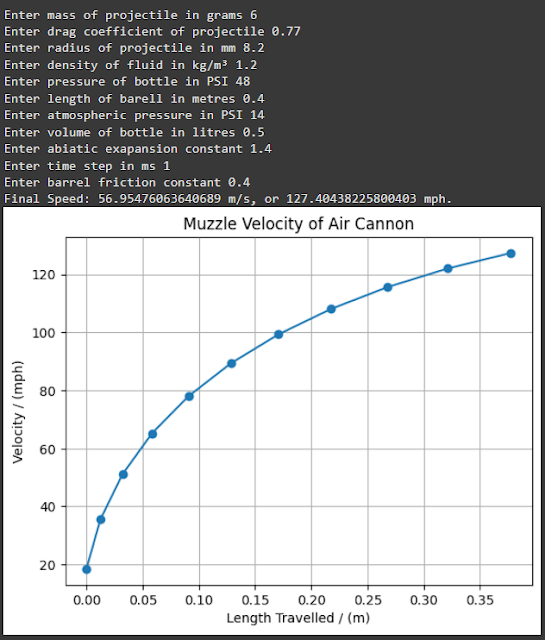
Enter mass of projectile in grams  12
Enter drag coefficient of projectile  1.4
Enter radius of projectile in mm  7.6
Enter density of fluid in kg/m³  1.2
Enter pressure of bottle in PSI  60
Enter length of barrel in metres  1
Enter atmospheric pressure in PSI  14
Enter volume of bottle in litres  0.5
Enter abiatic exapansion constant  1.4
Enter barrel friction constant  0.7
Enter time step in ms  1
Enter accuracy of output in decimal places 3
Enter baseline multiplier 1.23

 

The script attempts to generate a realistic muzzle velocity by having many inputted factors that are all used to draw a graph of the velocity of the projectile as it moves down the barrel.

 

The graph above is for a cannon with roughly the same parameters as the one I am building:

All inputs are first converted to SI base units so that the calculations can take place:

 

 

The surface area of the projectile is found. As pV is a constant, we can find this constant by multiplying the pressure in the bottle by the volume of the bottle. We can then set certain variables, such as velocity and drag force, to 0, allowing us to initiate the simulation.

We can then start a while loop, that incrementally adjusts the pressure as the gas in the bottle expands, adjust the drag force using the equationF=(1/2)⋅Cd⋅A⋅v², finds the changing velocity by finding the resultant force and dividing it by the mass of the projectile to find its acceleration, and other calculations such as kinetic friction and adiabatic temperature shifts that make the model as true to life as possible.

Finally, some code converts the arrays that hold all this data to a graph that clearly shows the decreasing acceleration of a projectile in an air cannon's barrel.

 

 

 Using this model, I could optimise for barrel length, bottle capacity, and other factors.

 

I started testing this in my living room. At this stage, I had no idea how structurally sound this system was - my primary concern was with the strength of the 3D print. Some sources stated 3D printed PLA filament with the same infill and wall count I used could handle up to 500psi, and an equal number of sources said it would fail at 30psi. For this reason, my test rig included a 3-sided metal box that would act as a shrapnel guard, so that if any plastic pieces failed, I wouldn't be filleted. 

 

 I used the packaging tape shown in the image to make the burst discs. I did this by cutting out a square, then laying it on the end of the pipe and cutting around it to form a circle slightly larger than the external diameter of the PVC pipe. I then pushed this firmly into the 3D print and locked it in place with the bolt.

This is the slo motion footage of the first test run. I used one layer of packaging tape, and used a marble wrapped in cellophane tape to make it seal perfectly with the pipe. I used an online software called Tracker Online to determine the speed of the marble. My bottle was used as a measurement device - as I knew the distance between the 7PM and 9PM markings, I would know the distance the marble travelled, then knowing the frame rate of the video, I can calculate the speed of the projectile.

 The tracking software gave me a speed of 22m/s . By inputting the data of the test shot, my software gave me this result:

The simulated and experimental values did not line up at all, with a 60.7% percentage error! This showed that the software needed tuning to match this specific air cannon's geometry. There are many factors I did not account for, such as flow rate due to the constriction in the nozzle, the expanding volume of the bottle as its filled, the leakage of air around the projectile and many others. Luckily, these all scale linearly, so I could replace all these factors with a multipler 'k', and find its value experimentally.

I did this with another test run:

And this time got a great matchup between the mathematical model, and the practical true result, with a multiplier value of 1.36:

 

 

Both results here give a value of around 35m/s as the muzzle velocity, with a percentage error now of only 3%. 

The reason for this model's creation is optimisation. In this scenario, we are presented with a certain bottle pressure, volume, projectile, etc. We can see that the highest velocity is achieved 0.11 metres down the barrel, before the speed drops off quickly due to friction. Therefore, for this specific cannon, a barrel of 0.11 metres in length would give the best results.

After building up some confidence in the design, I used 2 layers of packaging tape as the burst disc, so that it could build up more pressure. I also redesigned the way the burst disc was held. The current system was to crudely put tape on the end of the barrel and shove it into the 3D print. This worked 20% of the time, with the other 80% consisting of the barrel not making a good seal, or the tape breaking due to the stresses of pushing the barrel in so hard - I also managed to pull my wrist trying to push the barrel into the hole with tape around it; overall, it wasn't as professional as it could've been.

Many other air cannons use the sandwich design, where two metal plates have the burst disc in between them and squeeze down on it to create a seal. I cannot metal 3D print, since the facilities cost an insane amount, and I wanted to keep the budget of this project under 8 million pounds. This meant I needed to use existing metal pieces.

 

 

 I decided on some 25mm, thick plate washers. Of course, this could not fit in the 22mm hole, so I had to make my own lathe by placing the washers on a screw, and then holding my angle grinder to them in a way where they span. This way, I could grind the washers down to 21mm diameter evenly. The 25mm washer is shown on the right, and the two ground washers, with the O-ring used to separate them, on the left.

I pushed one washer into the PVC holder until the ridge, then placed the O-ring on top of it. For the burst disc, I wrapped packaging tape around the other washer and pushed it against the O-ring. I then pushed the PVC pipe in as hard as possible to get a perfect seal, even at 80psi. 

 

 Using this design, I could get up to 60psi before the burst disc ruptured. For the projectile, I hatched together an old drill bit tip pushed into a 3cm section of hose with an external diameter of 15.2mm, which is almost the same as the internal diameter of the barrel. I did many test runs off camera to perfect the multiplier mentioned before, to get around 1.23 for this specific cannon, burst disc, and washer design. I then used this test run:

 

 

 

 This video was uploaded and used in the tracking software, which gave a velocity of 48.7m/s:

 

As the plugged hose is made of rubber, it seals well and acts as a great projectile. The coefficient of friction between rubber and PVC is 0.7 for kinetic velocity, and the drag coefficient of the projectile was calculated to be 1.4, so by plugging these values into the model:

 

I got this result:

 

 

This mathematical estimate of 49.8 m/s lines up extremely well with the experimental value of 48.7 m/s, so I know that the model is tuned well for this use scenario (the percentage error for those who are interested is now 2%). Next, I went about finding the optimal barrel length and found it to be 0.862 metres from the mathematical model, giving a velocity of 59 m/s at the muzzle.

 

When testing with higher pressures, however, I got very different numbers. For an 80psi run in the same conditions, my barrel would have to be 106cm long. For a 70psi run, it would have to be 97cm long. I chose an arbitrary middle ground of 100cm, as my cheap bike pump maxed out at 79 psi when I was practically jumping on the handle.

A barrel of length any longer would be impractical; it would have to be completely straight in order to not have thinner and thicker areas, which would increase the overall friction inside the barrel. 

Finally, after installing the correct-length barrel, I got this run (the video was edited this way to make the projectile clearer):

 

After using the tracking software, I got a speed of 58m/s, which lines up with the 59m/s mathematical estimate with an accuracy of 98.3%. This concludes this project, as I could finally break the 100mph milestone with a large margin. The total cost for this project is calculated below, but I plan to make an even stronger cannon to try and break 300mph next time. Until then, please check out my other projects. Thank you for reading this far!

Project Costs: 

1.  3D printer filament: 87p
2. Sprite Bottle: £1.00
3. Shrader Valve: 50p
4. O-rings: 5p
5. Through-bolt: 10p
6. 2 Metal plate washers: 10p
7. Packaging tape used: 30p

Total: £2.92 

Extra costs - these represent the costs of everything else used to make this project; they are definitely not indicative of the cost of this project, but it can be useful to know what you will need outside of the raw materials to make something:

Other Costs: 

1. Bike pump: £7
2. 3D printer: £50 (used)
3. O-ring set: £1
4. Shrader Valve pack: £2.40
5. 3D filament roll: £9.40
6. Bolt set: £2.40
7. Washer set: £4.50
8. Packaging tape: £2.10
9. Wood glue for shrapnel shield: £5.50 
10. Super Glue: £1.10 

Total: £85.40 

 The 3D software used is Onshape.